Bentuk Integral Trigonometri dan Panduan Penyelesaian Soalnya
Bentuk Integral Trigonometri dan Panduan Penyelesaian Soalnya ~ Integral Trigonometri adalah salah satu bentuk integral yang dipelajari dalam dunia ilmu matematika. Integral ini berhubungan erat dengan tiga komponen trogonometri, yaitu : Sinus (sin), Cosinus (cos), dan Tangen (tan). Ketiga komponen trigonometri tersebut membentuk sebuah pertanyaan dalam alur integral, sehingga untuk penyelesaian pertanyaan tersebut juga memerlukan beberapa tahapan. Dalam kesempatan kali ini, kami akan membahas mengenai bentuk dari integral trigonometri dan panduan penyelesaian untuk soal yang mengandung struktur integral trigonometri.
Bentuk Integral Trigonometri
Mengenai bentuk dari Integral Trigonometri, ada 3 bentuk umum yang sering dipelajari. Ketiga bentuk umum tersebut memiliki struktur dan penggunaan komponen trigonometri yang berbeda. Berikut ini adalah bentuk dari ketiga Integral Trignometri:
- Fungsi Trigonometri Umum
Bentuk fungsi trigonometri umum yang biasanya digunakan untuk menyelesaikan persoalan intergral trigonometri adalah sebagai berikut:
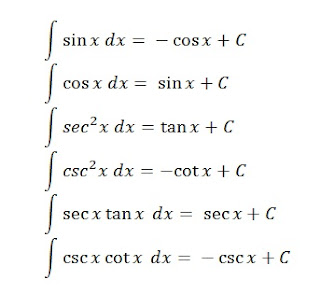 |
| Fungsi Trigonometri Umum untuk Integral Trigonometri |
- Fungsi Trigonometri Lanjutan
Bentuk dari fungsi trigonometri lanjutan yang dipergunakan sebagai pendukung integral trigonometri adalah sebagai berikut:
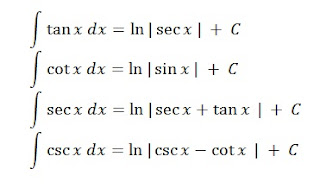 |
| Fungsi Trigonometri Lanjutan untuk Integral Trigonometri |
- Fungsi Invers Trigonometri
Bentuk dari fungsi invers trigonometri yang dipergunakan dalam penyelesaian soal integral trigonometri adalah sebagai beriku:
 |
| Fungsi Invers Trigonometri untuk Integral Trigonometri |
Sedangkan untuk bentuk trigonometri yang sering dipakai dalam struktur integral trigionometri di sekolah-sekolah adalah sebagai berikut:
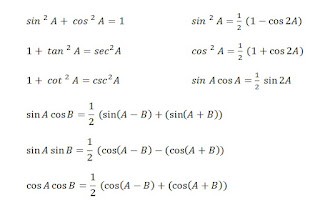 |
| Struktur Trigonometri untuk Integral Trigonometri |
Dalam proses penyelesaian soal-soal integral trigonometri, yang perlu kita lakukan adalah memecah bentuk soal menjadi bentuk struktur trigonometri yang sesuai. Jika sudah membentuk struktur trigonometri yang sesuai, maka aturan perpangkatan akan dapat diterapkan dalam soal.
Dalam penyelesaian integral-integral trigonometri, ada beberapa identitas trigonometri yang dapat dipergunakan. Berikut ini adalah beberapa identitas trigonometri yang erat hubungannya dengan integral trigonometri.
- Identitas Pitagoras
 |
| Identitas Pitagoras |
- Identitas Sudut Tengah untuk sin x
 |
| Identitas Sudut Tengah untuk sin x |
- Identitas Sudut Tengah untuk cos x
 |
| Identitas Sudut Tengah untuk cos x |
Panduan Menyelesaikan Soal Integral Trigonometri (Perpangkatan Sinus dan Cosinus)
- Perhatikan pada struktur perpangkatan soal. Jika terdapat pangkat dari sinus yang bersifat bilangan ganjil dan harga positif, maka simpan satu faktor dari sinus tersebut dan kemudian ubah faktor sisanya menjadi cosinus. Setelah itu lakukan ekspansi dan integralkan struktur baru tersebut.
| Tahap 1 Integral Trigonomoteri |
- Sedangkan untuk pangkat cosinus yang bersifat bilangan ganjil dan harga positif, maka simpan satu faktor dari cosinus tersebut dan kemudian ubah faktor sisanya menjadi sinus. Setelah itu lakukan ekspansi dan integralkan struktur baru tersebut.
| Tahap 2 Integral Trigonomoteri |
- Dan bila pangkat dari sinus dan cosinus keduanya berupa bilangan genap dan tidak negatif, maka gunakan secara berulang identitas di bawah ini, untuk mengubah integral menjadi perpangkatan ganjil dari cosinus. Dan hasilnya dilanjutkan seperti langkah poin kedua.
| Tahap 3 Integral Trigonomoteri |
Untuk lebih jelasnya mengenai penerapan rumus integral trigonometri tersebut, berikut ini kami sertakan contoh soal beserta pembahasannya. Semoga dapat membantu memperjelas penjelasan kami. [Contoh Soal dan Pembahasan]
Demikian ulasan singkat kali ini mengenai Bentuk Integral Trigonometri dan Panduan Penyelesaian Soalnya. Semoga bermafaat bagi adik-adik semua.











Post a Comment